Statistical Analysis and Results

Null hypothesis - There is NO relationship between a person's oral and axilla temperature.

Alternative hypothesis - There IS a relationship between a person's oral and axilla temperature.

Criteria to REJECT or Failure to reject the Null Hypothesis

• A statistical test uses the data obtained from a sample to make a decision to reject of fail to reject the Null Hypothesis


• Numerical value obtained from the statistical test - test value


• Alpha(α) refers to significance level - in the critical region

We have selected α at 0.05.

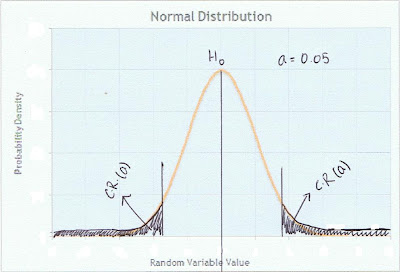
1. To reject the Null Hypothesis - the range of values of the test value MUST be in the critical region which indicate there is a significant difference


2. Failure to reject the Null Hypothesis - the range of value of the test value MUST be in the non-critical region which indicate that the difference was probably due to chance

In another words,

• if p value ≥ α, reject the null hypothesis.


• if p value < α, the null hypothesis should not be rejected.

The statistical test depends on the type of research question

• difference


• correlation
  

As our study is looking for a correlation between oral temperature and axilla temperature and both the variables are scale, we use Pearson's r to do the testing.

The table we created using SPSS for our results. (Data view)

(Please click to enlarge)

(Variable View)

(Please click pic to enlarge)

From the data above, we generated a scatter plot for oral temperature vs. axilla temperature using SPSS.


We also generated Pearson's R coefficient using SPSS.

The table shows Pearson's coefficient of .919.

The association is r=919 p=0.000, N=30.
Since it exceeds 0.8, it indicate that there are VERY STRONG, SIGNIFICANT and POSITIVE associations between a person's oral & axilla temperatures.

Linear Regression

Knowing that a relationship between a person's oral and axilla temperature exists, linear regression quantifies the relationship by having an equation predicting the person's oral and axilla temperature.

Oral temperature=1.051*(axilla temperature)-1.337

Re-state final statement:

Thus, we accept the alternative hypothesis that there is a positive and significant between a person's oral and axilla temperature.